Десять цифр  
 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
служат алфавитом языка чисел,
которым сейчас пользуются практически на всем земном шаре.
Этот язык называется десятичной системой счисления.

Но не везде и не во все времена люди пользовались десятичной системой.
И, между прочим, с чисто математической точки зрения она не имеет специальных преимуществ перед другими возможными системами счисления.

Почему десятичная?

Наши предки брали за основу 10 пальцев рук.

Поэтому считается, что именно счет по пальцам рук положил начало системе, которая теперь кажется нам чем-то само собой разумеющимся. 

Однако такое господствующее положение
десятичная система счисления заняла далеко не сразу.
Разные народы в разные исторические периоды пользовались различными системами счисления.

У ряда африканских племен была распространена пятеричная система счисления. Опять же это может быть связано со строением человеческой руки - первоначальной «счетной машины».

У ацтеков и майя, народов населявших в течение многих столетий обширные области американского континента, а также и у кельтов, населявших западную Европу, начиная со второго тысячелетия до нашей эры, была принята двадцатеричная система. Некоторые следы этой системы сохранились в современном французском языке, например «восемьдесят» по-французски quatre-vingts - буквально «четырежды двадцать», а в денежной системе 1 франк = 20 су.

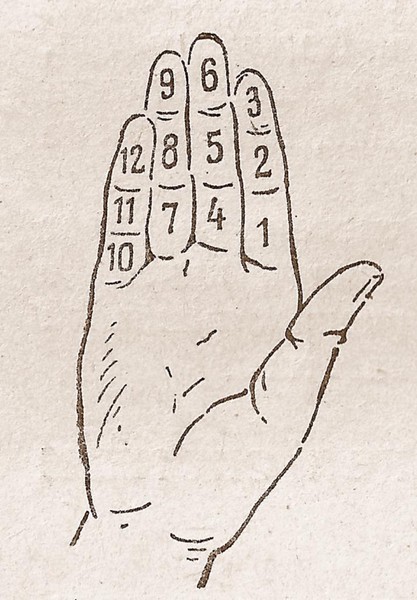
Происхождение двенадцатеричной системы также связано со счетом на пальцах. Четыре пальца руки (кроме большого), имеют в совокупности 12 фаланг, по этим фалангам, перебирая их по очереди большим пальцем, и ведут счет от 1 до 12. Затем 12 принимается за единицу следующего разряда и т.д. 

Двенадцатеричными дробями пользовались еще древние римляне.

Дробь 1/12 римляне называли унцией.

Шведский король Карл XII
(тот самый, которого разгромили русские войска под Полтавой в 1709 г.)
пытался узаконить двенадцатеричную систему счисления.

Во Франции в конце XVIII века также всерьез обсуждалась идея перехода к двенадцатеричной системе счисления.
Кто не слыхал, как вместо числа
«двенадцать» мы говорим «дюжина»?!

Многие столовые предметы: ножи, вилки, ложки, бокалы, тарелки, чашки считают именно дюжинами, а вовсе не десятками. Вспомните, что сервиз бывает, как правило, на 12 или на 6 персон.

В этой системе счисления:
«гросс» - «дюжина дюжин», а
«масса» - «дюжина гроссов».

Возможно в таком значении слова «масса» и лежит корень таких выражений, как «масса дел», «масса людей» и т.п.

Если же говорить о народах, то у англичан
в системе мер:
1 фут = 12 дюймам,
1 дюйм = 12 линиям, а
1 линия = 6 точкам.
в денежной системе:
1 шиллинг = 12 пенсам.

Еще одна система счисления - шестидесятеричная.

Известно, что в древнем Вавилоне
существовала именно такая система счисления.

Некоторые историки считают, что произошло смешение двух племен, одно из которых пользовалось шестеричной системой, а другое - десятичной. Существуют и другие гипотезы, но они также не могут быть достаточно обоснованными. Однако эта система в некоторой степени сохранилась и до наших дней.

Например в системе времени:
1 час = 60 минутам,
1 минута = 60 секундам,
а также в системе измерения углов:
1 градус = 60 минутам,
1 минута = 60 секундам.

Итак основа перечисленных систем счисления, кроме шестидесятеричной, связана с тем или иным способом счета по пальцам рук (или и рук, и ног) - т.е. имеют «анатомическое» происхождение.

Многие первобытные племена пользовались
двоичной системой счисления.

В этой системе счисления все числа записываются
с помощью двух знаков: 0 и 1.

По-настоящему развил ее немецкий математик,
философ, историк, дипломат, изобретатель

Готфрид Вильгельм Лейбниц (1646 - 1716).



Лейбниц считал нуль символом пустоты, а единицу - символом материи.

Со времен Лейбница до недавнего времени двоичную систему считали лишенной практической ценности, т.к. запись чисел в двоичной системе слишком длинна и неудобна в использовании.

Давайте немножко посчитаем...    

"НЕОБЫКНОВЕННАЯ ДЕВОЧКА"

Ей было тысяча сто лет,
Она в сто первый класс ходила,
В портфеле по сто книг носила -
Всё это правда, а не бред.
Когда пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали
И десять тёмно-синих глаз
Рассматривали мир привычно...
Но станет всё совсем обычным,
Когда поймёте наш рассказ.
(А.Н.Стариков)

Какие числа в стихотворении вы увидели? 1100, 101, 100, 10, 1

Все эти числа записаны с помощью только двух цифр: 0 и 1.
Значит все эти числа - числа двоичной системы счисления.

1 хвост - тут всё ясно. Это 1 и  в десятичной системе счисления.
10 рук - это в двоичной системе, а в десятичной, это соответствует числу 2.
100-ногий щенок, конечно же имеет 4 лапы в десятичной системе счисления.
101 класс - тоже, надеюсь, ясно - 5 класс в привычном понимании.

Сколько было лет девочке в переводе с двоичной системы счисления в десятичную?



Вот таким способом можно перевести число из десятичной системы счисления в двоичную:

В XX веке двоичная система стала одним из истоков произошедшей компьютерной революции. Ячейка памяти ЭВМ может находиться только в одном из двух состояний. Технически все просто: 1 - проходит ток в полупроводниковом элементе, 0 - ток не проходит. Состояние элемента «проходит ток» и «не проходит ток» могут сменять друг друга за миллионные доли секунды, что позволяет производить арифметические действия над двоичными числами с неимоверной скоростью.

"Почём кило байтов?"

В десятичной системе счисления:

В современной математике есть раздел - теория информации. 
В частности, эта теория определяет способ измерения количества информации 
и единицу измерения называет "бит". 

"За один байт восемь битов дают"

Эти приставки тоже всем знакомы:
"кило-" - тысяча,
"мега-" - миллион,
"гига-" - миллиард.




Программисты тоже используют эти приставки, но в несколько в другом значении!
А причина в том, что  в двоичной  системе  счисления,  так называемые  "круглые" числа - это не степени числа 10, а степени числа 2 !!!

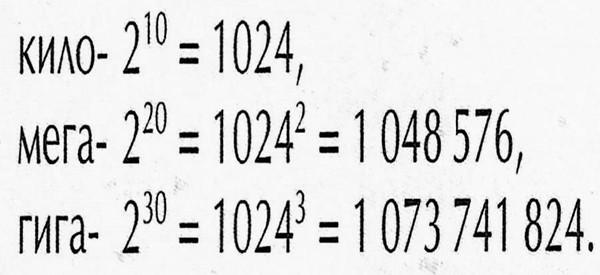А, между прочим, знаете что означает слово "ГУГОЛ"
и кто его придумал ?

Среди внесистемных названий больших чисел

"Гугол" означает 10 в степени 100!
А тогда что такое "Гуголплекс"?
Это 10 в степени гугол!
Однажды американский математик Эдвард Каснер спросил
своего девятилетнего племянника,
как бы он назвал это число, и тот ответил: "Гугол"

Все системы счисления, о которых шла речь, являются

позиционными.

Преимущество позиционных систем счисления - это не только запись больших чисел с помощью сравнительно небольшого числа знаков, но и, прежде всего - простота и легкость выполнения арифметических операций над числами.

                    


Примером непозиционной системы счисления
служит запись чисел римскими цифрами.

          I - единица,
  V - пять,
      X - десять,
             L - пятьдесят,
C - сто,
         D - пятьсот,
        M - тысяча.

Каждое число представляется, как комбинация символов.
Смысл каждого символа не зависит от того места, на котором он стоит.